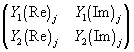
(a)
(b)

(c)
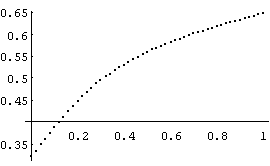
(d)
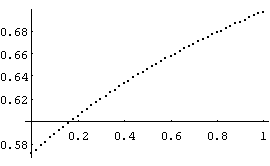
(e)
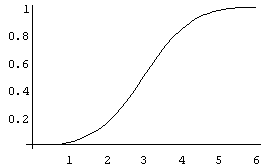 (f)
(f)
Figure 1 Curves produced by V7 and a CNO curve
Psychophysics, the study of human responses to physical stimulation, was dominated first by Fechner's logarithmic law, and then by Stevens' power law. Both laws assume that changes in responses within the organism are directly proportional to changes in the level of external stimulation. While useful in certain contexts, these laws do not do justice to the full complexity of human psychophysical response; and many researchers have pointed out the need for a more sophisticated mathematical psychophysics.
One promising direction, in this regard, is nonlinear science. In recent studies of the brain, neuroscientists have begun to realize that perceptual processes often reflect patterns found in non-linear dynamics. Walter Freeman, for example, has shown that some apparently random perceptual processes actually have deterministic dynamics, with chaotic attractors. In 1991, he published a paper "The physiology of perception," reporting experiments in which he trained rabbits to recognize several different smells. He attached electrodes to the olfactory bulb surface of the rabbits in order to collect sets of 60 to 64 simultaneously recorded electroencephalogram (EEG) tracings. In the experiments, the EEG tracings from the electrodes are "as unpredictable and irregular as freehand scrawls" [1]. Yet they manifest perceptual information. This can be shown by "phase portraits" which are made from the EEGs generated by a computer model of the brain. In Freeman's experiments, the phase portraits reflect the overall activity of the olfactory at rest and during perception of a familiar scent. As he states, "Resemblance of the portraits to irregularly shaped, but still structured, coils of wire reveals that brain activity in both conditions is chaotic: complex but having some underlying order." He also indicates that the olfactory EEGs are closer to being periodic during perception than during rest.
Recognition of the complexity and nonlinearity of perception has led some researchers to propose the use of non-linear dynamics models for describing the perceptual processes. Most impressively, Robert Gregson has developed a non-linear psychophysical function he calls the "gamma recursion" and has conducted many computer simulations of psychophysical phenomena using the model. The model has been shown to demonstrate many complex, psychophysically plausible behaviors [2].
Gregson's argument for the non-linearity of the perceptual processes is as follows: "It is known that sensory pathways at higher cortical levels can be multiple, recursive, perseverative, and nonlinear. There are also grounds for treating large aggregates of connected neural structures as capable of generating nonlinear and chaotic dynamics as part of their normal functioning. Given those constraints, a cubic complex polynomial recursion gamma was defined, which satisfies the criteria stipulated. This model generates, intrinsically, both observable response and unobservable (theoretical, deterministic) noise at the same time, without excluding the fact that additional stochastic noise can also exist in the system modeled" [3].
This paper reports an attempt to replicate several of Gregson's results. In many cases my specific numerical results do not agree with Gregson's; however, the basic qualitative pattern of the results is the same. In accordance with Gregson, I conclude that the gamma recursion is a viable tool for studying the nonlinearity underlying human psychophysical responses.
The "original" (one-dimensional) gamma recursion is introduced for the first time in 1988 in Gregson's book Nonlinear Psychophysical Dynamics. It is defined as
Yj+1 = -a (Yj - 1)(Yj + ie)(Yj - ie), i2 = -1
where a is real (Re), ie is imaginary (Im), Y is complex (Re, Im), and the boundary conditions are 0 < Y(Re) < 1, Y0 = (), .5, < 10-8 (i.e. the initial condition .5 + 10-9 i), 2 < a < 4, 0 < e < .5, and very approximately ae < 1.7 in the region of .5 < e < .7 to avoid the explosive condition [2].
An interesting point of this function is that with a little modification of the parameter value a, the gamma recursion can model the psychometric function that is a CNO-like function. For example, one of the modification in parameter value a of the gamma, he calls [[Gamma]]V7, is defined as
0 < U < 1, amin < a < 4, e fixed
(number of iterations) fixed, Y0 = .5 , [[epsilon]] (complex)
a = amin + (3.99 - amin) U,
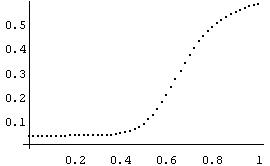
where U is the stimulus, and Y(Re) is the response [2]. The shapes of these functions after 10 iterations ( = 10) varies completely as e changes from .03 to .3. Figure 1 shows the change over that range. And with amin = 3.2 and e = .15, the function shows the pattern of a psychometric function.
(a)

(b)

(c)

(d)

(e)
 (f)
(f)
Figure 1 Curves produced by V7 and a CNO curve
Figure 1 (a)(e) shows the curves produced with the real part of the gamma recursion after 10 iterations with a = 3.2 + .79 U (amin = 3.2), 0 < U < 1. (a) e = .03,
(b) e = .1, (c) e = .15 (shows a CNO-like curve), (d) e = .2, (e) e = .3.
Figure 1 (f) shows the cumulative normal ogive, which is a psychometric function generated by psychophysical data.
The x-axis represents the stimuli, and the y-axis represent the responses.
The values on the graphs are scaled for graphing purposes.
The gamma recursion models the transformation from stimulus to response in a single channel. However, to represent, for example, bilateral stimuli inputs such as fully vision or audition requires two dimensional inputs. For this purpose, Gregson introduced the two-channel gamma model he calls the 2[[Gamma]]. The system 2[[Gamma]] is classified into two cases by the difference of their cross-coupling between channels; the first case is simpler, however, it would not generate the irregularity which might, for example, characterize some visual illusions [5]. The 2[[Gamma]] can be extended to more general vectorial and lattice models called n and (nn).
The descriptions of Case 1 and Case 2, and the model are extracted from Gregson's book n-Dimensional Nonlinear Psychophysics:
Case 1: If the (Im) output of Yobs, (which is the value of Y after recursions), is taken as interpretable as a form of internal noise, as has been shown to be plausible in other contexts (for example, it exhibits intermittency), then take the total within-loop noise at any step in the recursion to be the union of the component noises. So in each cycle the two Y(Im) are replaced by the term max(Y1,j, Y2,j)(Im) and as the (Im) components go into limit cycling more readily (that is, at lower system parameter values) than their (Re) counterparts, the effect will depend crucially on the set of values (a1, e1, a2, e2) (Campbell and Gregson, 1990). It can be shown, by simulation, that high (e1, e2) values induce some curious effects for large Uj (inputs); a paradoxical "turn-over" effect in
U Yobs graphs for at least one component is observable (Gregson and Britton, 1990). At the same time the other component may create a monotonically decreasing graph of U Yobs.
For a double loop put, for case 1, where the two dimensions are denoted by h and i suffices,
Yhij(Im) = max(Yhj(Im), Yij(Im))
and then define
Y*hj = (Yhj(Re), Yhij(Im))
and
Y*ij = (Yij(Re), Yhij(Im).
Case 2: A second cross-linkage is possible if the e terms are made to be functions of the a terms in the opposite dimension. This represents a process of mutual inhibition. Each dimension is desensitized to differences in its own input as the input to the other dimension is increased, viz.:
eh = h ai-1, ei = i ah-1,
where h > 0, i > 0, and 2.6 < amin < 4.4 is a working range for 0.05 < e < 0.40, and approximately .20 < < 1.2 will avoid the explosive condition of ae > 1.7.
The advantage of writing e in terms of and a is that the number of parameters in the model can be reduced by one; e1 and e2 are removed and is introduced, with
h = i = . For case 2, additionally we have
Yh(j+1) = -ah (Y*hj - 1)( Y*hj - ih (ai)-1)( Y*hj + ih (ai)-1)
and correspondingly
Yi(j+1) = -ai (Y*ij - 1)( Y*ij - ii (ah)-1)( Y*ij + ii (ah)-1).
See figure 2 for better understanding of the model.
Pure Delay Filter
Sensory 1
U1 Dimension a1 e1 Yobs,1
One
Inputs Real Observable
Sensory 2
U2 Dimension a2 e2 Yobs,2
Two
Figure 2 Diagram of cross-coupling used in 2[[Gamma]] case2, the labelled 1, 2 are themselves the recursions.
To show non-linear psychophysical dynamics using his 2[[Gamma]] , Gregson has carried out several studies with psychophysical data. In one study, Gregson [3] applied 2[[Gamma]] to approach Fechner's Paradox. Fechner's Paradox is where apparent brightness of an object viewed binocularly can, under conditions where the input to one eye is diminished by filtering, be less than its brightness viewed monocularly by the unfiltered eye. The same phenomenon in pooling two sensory inputs has its analogues in audition and in olfaction. In this case also, Gregson points out that the analysis with a linear model makes a limited success; "The idea that unidimensional stimuli coalesce vectorialy to generate mixtures of two stimuli, in terms of intensities, has been used with limited success in modelling various sensory modalities; in the context of Fechner's Paradox it was advanced by Curtis and Rule (1978). It is now known that it fails in vision (Irtel, 1986), as it also fails in olfaction (Gregson, 1986)" [3]. Using his 2[[Gamma]], case2, however, Gregson states that "great variations in the form and scatter of isointensity (brightness or loudness) distributions occur in the region of a1/a2 [two input stimuli] and a model should predict such local instability, as well as predicting much clearer trends in the midrange where a1 and a2 approach equally" [3]. Gregson's results indeed predict the instability.
I replicated Gregson's research using the "original" gamma recursion with the same parameter values of a and e. While I obtained several results that were consistent with Gregson's, there were a number of significant discrepancies. Figure 3 shows the chaotic behavior of the gamma recursion with certain parameter values a, and e, where my results support Gregson's findings. Figure 4 shows result of the gamma recursion for some parameter values a and e where Gregson's results are not supported.
(a)
(b)
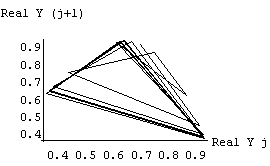
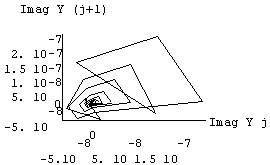
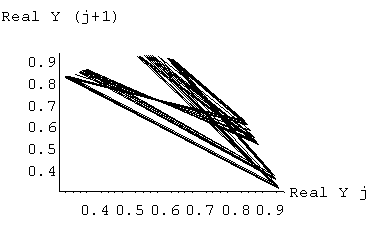
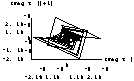
Figure 3 Phase portraits showing chaotic behavior in the real and imaginary domain for the gamma recursion with specific parameter values of a and e.
(a) parameter values a = 5.75 and e = 0.2
(b) parameter values a = 4.20 and e = 0.4340
Each point is plotted as an x-y coordinate where x-axis is the real/imaginary value of Y at the jth iteration and y-axis is the real/imaginary value of Y at the j+1th iteration except the third one of (b). In this case, x-axis is the real value of Y at the jth iteration and y-axis is the imaginary value of Y also at the jth iteration.) .
Each successive point is joined, providing a trace of the output of the gamma recursion across iterations. Complex traces reflect chaotic behavior. The values after each iteration are unique and seem random. However, they are confined within a certain region forming a pattern that is called a "strange attractor".
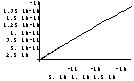
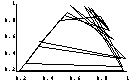
Figure 4 Phase portraits showing the dynamics in the real and imaginary domain for the gamma recursion with specific parameter values of a and e.
Comparison is made between Gregson's results (left) and mine (right).
(a) parameter values a = 3.31 and e = 0.2. With these parameter values, the gamma recursion converges to 0.337403 + 4.59355 10-16i. Therefore Gregson's result is not accurate.
(b) parameter values a = 6.543 and e =0.0. The result I obtained (right) shows the trace of up to 29 iterations. At the 30th iteration, the real value of Y escapes the region of (-1,1), and therefore causes the explosion.
In order to probe the characteristics of the one dimensional gamma recursion further, Gregson also conducted an experiment to see how the Yobs (observation, the real component of Y) varies over the parameter values a and e for fixed recursions. His reasoning for this action is as follows;
"If [2.2] [the gamma recursion] runs a limit of recursions then the result is Yobs, which as defined is complex. It may be single-valued or oscillating in one or both components. For a fixed , over the parameter space {a, e} we may thus construct a bivariate response surface PY, of { Yobs, a, e}, and this at any point will have four values; minY(Re), maxY(Re), minY(Im), maxY(Im). There are thus in theory four distinct response surfaces, but they are not distinguishable at all (a, e) points, and not all of equal interest" [2].
Figure 5 shows Gregson's results of PY, at = 1000 and = 1001 which are the surface graphs of Y at 1000th iteration and 1001st iteration over the region of
2.5 < a < 6.5 and 0.0 < e < 0.8. Figure 6 shows my results with same conditions as Gregson's. My results are clearly different to those of Gregson's.
(a)
(b)
Figure 5 Gregson's results for the gamma recursion after 1000 (a) and 1001 (b) iterations with parameter values over the region of 2.5 < a < 6.5 and 0.0 < e < 0.8.

(a)

(b)
Figure 6 My results for the gamma recursion after 1000 (a) and 1001 (b) iterations with parameter values over the region of 2.5 < a < 6.5 and 0.0 < e < 0.8.
In addition to replicating experiments reported in Gregson's books, I also reviewed Gregson's unpublished paper "The second eigenvalue in 2 gamma case two dynamics and dimensionality of output". In the paper, Gregson examines the dynamics of a local region in 2[[Gamma]] by utilizing the instability of the second (smaller) eigenvalue of the system. Then he applies the theory to Eisler cusps, a peculiar phenomenon observed in the task of estimating dimensions of rectangles. As Gregson observes, "When subjective width with varying heights are plotted against shape (ratio of height over width) with physical width as parameter, curves with cusps are obtained" (Eisler, Eisler and Gregson, 1995). It has been named a `cusp'" [6].
In his study of the Eisler cusp, Gregson studies the eigenvalues of 2[[Gamma]] Case 2 by constructing a 2 x 2 matrix of the form
Y2,j =
[[sigma]]2* = log10(2104+1.0)
to show detailed contour plot. In the paper, he shows six results of those
maps (three different a1 values over two different
iterations), and suggests those "bubble" like figures (see figure 7) are
connected to the cusps in the rectangle perception.
The review I contributed was not concerned with his theoretical
interpretations, but simply with the contour maps of those second eigenvalues.
Of those six maps, Gregson found five to show bubbles; however, in my results,
only one of them showed bubbles (namely a1=3.2 and =20).
Moreover, even for this case, the map I found does not show much resemblance to
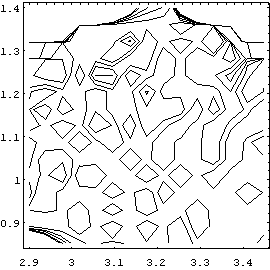
Gregson's map. Figure 7 shows the comparison between Gregson's result (a) and
mine (b).
(a)
(b)
Figure 7 Contour plots of the second eigenvalue of 2[[Gamma]] over 0.85 <
< 1.40, and
2.90 < a2 < 3.45, a1=3.2 and =20.
(a) Gregson's result, and (b) my result. They do not have any resemblance, but
they both show the trace of "bubbles".
Neurophysiological and psychological research suggests that perceptual
processes are best described by non-linear dynamics. With this in mind,
Gregson has developed a model of non-linear psychophysical dynamics based on
the gamma recursion. Here I have reported some attempts to replicate Gregson's
computational results.
Some of the results using the gamma recursion in the present research are
inconsistent with those obtained by Gregson using the same parameter values.
However, the present results confirm Gregson's qualitative conclusions. The
gamma recursion displays a variety of complex behaviors, including chaotic
dynamics; and it does plausibly simulate psychophysical response functions.
The discrepancy between the results of Gregson and myself may be due to the
levels of numerical precision. Gregson used FORTRAN to run his experiment which
is precise to 16 decimal places [7]. My research used Mathematica which
calculates with infinite precision. Therefore differences between the two
studies may reflect the rounding error inherent with the use of FORTRAN.
The present research could readily be extended into a series of experiments
that constitute the basis for a doctoral thesis. In particular, future
research would determine whether the non-linear gamma recursion model can
account for the perception of several visual illusions which have not been
modeled in the past by linear models. If the gamma recursion is able to model
the visual illusions, then non-linear dynamics would be a good model for
understanding a wide range of basic perceptual processes. Furthermore, it may
provide a tool for understanding higher level perceptual processes.
References
[1] Walter J. Freeman. The physiology of perception. Scientific
American.
February 1991, pp 34-41.
[2] Robert A. M. Gregson. Non-linear Psychophysics. Lawrence
Erlbaum
Associates Publishers, Hillsdale, 1988.
[3] Robert A. M. Gregson. Nonlinear psychophysics and Fechner's
Paradox.
Mathematical and Theoretical Systems, pp 207-218,
Elsevier Science
Publishers, 1989.
[4] Robert A. M. Gregson. The size-weight illusion in 2-D nonlinear
psychophysics.
Perception & Psychophysics. 1990. 48(4), pp
343-356.
[5] Robert A. M. Gregson. n-Dimensional Nonlinear
Psychophysics. Lawrence
Erlbaum Associates Publishers, 1992.
[6] Robert A. M. Gregson. The second eigenvalue in 2 gamma case two
dynamics and dimensionality of output. Unpublished draft paper, June
95.
[7] Robert A. M. Gregson. Private communication, August 1995.