Schizophrenia and the Family II: Paradox and Absurdity in Human Communication Reconsidered

Parts of this paper were presented at the annual meetings of the Society for Chaos Theory in Psychology and Life Sciences, Boston, MA, August, 1998, and the International Congress of Psychology, Montreal, Canada, August, 1996. Address correspondence to Matthijs Koopmans; 520 West 114 Street, #54; New York, NY 10025; USA, or to MKoopmans@aol.com.

Recent developments in Nonlinear Dynamical Systems theory enable us to address a number of unresolved issues in connection with Gregory Bateson's double bind theory. This paper conceptualizes the origin of double bind interactions in terms of bifurcations, which occur when interaction in family systems becomes highly unpredictable, and in terms of situations in which the newly emerging attractor is incompatible with the processes through which the system maintains its integrity. This conceptualization forges previously unexamined links between double bind and the differentiation of social systems, between double bind and autopoiesis, and between double bind and chaotic behavior. It is further argued in this paper that our ability to describe double bind in terms of Russell's paradox does not require that we assume a theory of logical types.

About forty years ago, Bateson, Jackson, Haley, and Weakland (1972/1956) published a paper entitled 'Toward a theory of schizophrenia'. This paper generated considerable interest because of its radical claim that the symptoms of schizophrenia might be the result of the internalization of contradictory patterns of communication in the family. Bateson et al. called such patterns double bind interactions. It was hypothesized that the consequence of prolonged exposure to double bind is that people gradually learn to perceive their universe in double bind patterns, and act on their environment as if every input from the environment is contradictory. This style of responding, it was argued, characterizes schizophrenic symptoms.

Double bind interactions are defined as conflicting messages conveyed more or less simultaneously, as in the situation, well known from Bateson et al.'s paper were a mother tells her son that she loves him while at the same time turning her head away with a look of disgust. In this example, the mother conveys two messages to the son: one of love, conveyed verbally, and one of disgust, conveyed non-verbally.

The results of empirical research on Bateson et al.'s double bind theory have not been deemed very encouraging (Abeles, 1976; Olson, 1972; Schuham, 1967). Extant research has been criticized, however, for the fact that the operationalization of the double bind construct has been inadequate (Abeles, 1976; Haller, 1989; Koopmans, 1997; Olson, 1972; Watzlawick, 1963). Meanwhile, the scientific community has more or less accommodated to the fact that while double bind may be a useful heuristic model for therapists and social workers, it is deemed unsuitable for empirical scrutiny because of the elusive nature of the proposed family dynamics (Abeles, 1976; Haller, 1989).

Recent developments in nonlinear dynamical systems models have made it possible to be more explicit about some of the dynamical constructs underlying double bind theory. The purpose of this paper is to bring out some of these implicit notions with the help of the contemporary Nonlinear Dynamical Systems vocabulary, and further specify some of the more elusive constructs of the theory. In this endeavor, we rely on the following basic NDS notions: (1) Positive and negative feedback in family communication, (2) The unexamined link between schismogenesis and double bind in Bateson's writings, (3) Bifurcation and second order change in families, (4) Autopoiesis, and (5) The logical underpinnings of paradox and contradiction. For a justification of our concern with double bind theory to examine the relationship between schizophrenia and family dynamics, see Koopmans (1997).

One of Bateson et al.'s most central contentions is that in order to understand the self regulatory aspect of human communication, one needs to consider its moment to moment instances in light of the relational context in which they occur. Any communicative expression affects the relational context in which it takes place, while this relational context, in turn, is modified and affected by subsequent communicative exchanges. In the interaction between parents and children, for example, there is a history of communicative expressions according to which the parent - child relationship is defined. New exchanges at a given point in time take that interactive history into account while at the same time affecting that history either through consolidation, or attempts to change the relational context. Communicative expressions are concerned with the relational context by definition because they shape the future context, and their occurrence is made possible by the extant relational context. There is an ongoing interrelationship, in other words, between individual communicative expressions, and the relational framework within which these expressions take place, i.e., there is a feedback loop, which connects individual communicative expressions to their relational context (see Figure 1).

Bateson made a distinction between two levels of communicative behavior: a purely substantive level, which refers to the use of communication to exchange information for its own sake, and the metacommunicative level, which refers to the self-regulatory function of communication in social systems. Effects of communicative expressions on the relational context need to be understood on the metacommunicative level. An example where this self-regulatory aspect is fairly explicit is the following exchange between a mother and her daughter:

More directly related to double bind theory is the following episode, with which Bateson et al. illustrate how information can be conflicting on the verbal and nonverbal level:

The mother's response to the son is highly ambivalent in that she is not accepting toward the son's affection, and then condemning him for his withdrawing response to her non-accepting behavior. Bateson saw this exchange as a typical example of double bind interactions: the initial lack of acceptance on the part of the mother is invalidated by her condemnation of the son's withdrawing response, and the incongruous emotions are played out on the verbal as well as the nonverbal level.

This example also illustrates how difficult it is to interpret interactive episodes between individuals without being familiar with the relational context in which these episodes take place. For the participants in this exchange, the understanding of the communicative expressions described here occurs in light of previous communication.

In his early work, Bateson referred to this layered quality of human communication by making a distinction between 'report' and 'command' (Olson, 1972). Report refers to the content of a message, and command defines the nature of the relationship between the participants exchanging the message. Olson suggests that if we consider report and command as the two different logical types, we can define double bind as a situation in which the report and command components of a message relay conflicting information. "A relationship constitutes the context, which is of a different 'logical type' from the component tasks or specific messages that may be found within the relationship. Double binding involves an impasse in which a relationship is partially invalidated or contradicted by new events within the relationship (Wynne, as quoted by Olson, 1972, p. 81.)" The notion that double bind invalidates relationships has been further developed by Sluzki, Beavin, Tarnopolsky and Verón (1967), who refer to these contradictions as transactional disqualification. The 'new events within the relationship' presuppose that a certain type of relationship between two participants has been previously established, and that the content of new messages exchanged between the participants challenges the existing relationship between participants. The presupposition of that relation, which makes the communication possible in the first place, is challenged by the actual content of the messages exchanged at a particular point in time, and which presupposes a different type of relationship.

Some metacommunicative expressions are consistent with the relational context, in which they occur, while others are inconsistent. Expressions of animosity can occur in a relational framework, which is generally loving, and loving expressions can occur in a relational framework which is generally hostile. If metacommunication is consistent with the relational framework in which it occurs with respect to some variable, we refer to the feedback as negative. Feedback of this kind reduces the amount of variability in the communicative behavior taking place within that frame. We call this type of feedback negative feedback. Conversely, feedback, which increases the amount of variability in communicative behavior, is called positive feedback. Positive feedback enhances fluctuation in the system, while negative feedback dampens fluctuation (Gottman, 1993; Hinde, 1995; Hoffman, 1971; Koopmans, 1998a, 1998b; Proskauer, 1996; Whitchurch & Constantine, 1993). For example, unloving utterances within a loving context can be seen as positive feedback, while unloving utterances in an unloving context can be seen as negative feedback.

Feedback and stability in the system are closely related: ongoing positive feedback cycles produce high fluctuation, structural change, or, in extreme instances, chaotic behavior. Ongoing negative feedback cycles, on the other hand, have a stabilizing effect on the system. High variabililty in communicative expressions indicates lack of stability. Whether feedback is defined as positive or negative depends on whether fluctuation are increased or reduced in such situations. Ongoing positive feedback cycles in this situation would result in chaotic behavior, behavior, that is, where fluctuation is extreme, and interactive behavior becomes highly unpredictable as far as 'lovingness' is concerned (Koopmans, 1998a).

As Bateson's example above indicates, communication can also be ambiguous on the metacommunicative level. In some situations, an affectionate remark is immediately followed by a hostile remark, or there is a going back and forth between affection and hostility. In such situations, the relational frame will most likely determine where communication will gravitate. In the exchange between mother and son cited above, a more prolonged interaction between the two would gradually reinstate their generally loving, or hostile, relationship. In such situations, the extant relational frame disambiguates communication by allowing participants to interpret ambiguous expressions in terms of this existing frame.

It is possible that a relational framework itself is ambiguous in the sense that is does not resolve whether the relationship is loving or hostile. In such situations, only sustained interaction of a given type, but not of any other type, would gradually help disambiguate the framework. As far as Bateson's example above is concerned, we know very little about the relational context into which we should place these exchanges, but it is not difficult to recognize the ambiguity in this particular exchange on the 'lovingness' continuum. We might imagine that prolonged exchanges of this nature produce a relational context which itself is highly ambiguous, making it difficult to interpret new utterances in an unambiguous manner. If, on the other hand, the interactional flow is consistently loving, or consistenly unloving, this will disambiguate the frame, and reduce fluctuation. A continuous going back and forth between loving and unloving would in effect maintain the ambiguity or high fluctuation in the system. These kind of long-term consequences of ambiguity are a matter of central concern to double bind theory.

Bateson was mostly concerned with double bind in his discussion of the cause of schizophrenia, while he discussed schismogenesis in his anthropological papers (Bateson, 1972/1935). There is good reason to consider the two constructs as part of a single dynamical theory and examine their connection. We need to determine whether frequent double bind interactions are part of a differentiation process in the system. The following section is concerned with schismogenesis, or systemic differentiation. It follows Bateson's line of reasoning step by step.

Schismogenesis, or progressive differentiation (v. Bertalanffy, 1968), refers to a growing autonomization of different components of a system. Bateson identifies two different types of differentation, namely complementary differentiation and symmetrical differentiation. Complementary differentiation occurs when two systems, here system A and system use one frame (P here) when the exchange of information goes from A to B, and another frame (U) when the exchange of information goes from B to A (see Figure 2). If two systems are differentiated in a complementary fashion, the members within system A also use a different frame (say, L) to exchange information amongst themselves, as the members within system B, who use R when they exchange information amongst themselves.

An example of complementary differentiation occurs in the family if you define the different components of the system as consisting of the following components. A spousal alliance (system A), a siblings alliance (system B), a spousal frame of interaction (L), a siblings frame of interaction (R), a parent to child frame (P), and a child to parent frame (U). The two systems A and B are kept separate, to the extent that the differences between the frames P and U, and the differences between L and R are maintained in the individual communicative exchanges (p, u, l, and r), which each address their respective frames. The feedback function shown in Figure 1 states the general case where frame X and expressions x_i could stand for any of the frames and expressions discussed in this example.

On account of the feedback relationship defined above, we could argue that within each frame, the conforming utterance both reflect, the frame as well as behaviorally reinforce it. . The respective use of U and P by the two systems depicted in Figure 2 reinforces the boundary between the two systems. In addition, if individuals in A use L in exchanges with each other, while in B they use R, this difference further illustrates the difference between the two constellations. Individual communicative expressions, which conform to this pattern, are defined as negative feedback in this example, because they reduce fluctuation by not bringing other elements into the interactive behavior. Fluctuation is produced by individual expressions, which deviate from the pattern. In this example, if A invokes U in response to B, which challenges the pattern in Figure 2, we could speak of positive feedback because this response takes the communicative trajectory away from the extant attractor regime. Exchanges within A and B can dampen or enhance fluctuation in the same manner. The differentiation of A and B enables the two systems to maintain a status of autonomy from each other, i.e., they remain distinct from each other. Positive feedback, in this scenario changes this constellation, for example by letting A and B drift apart, or by letting A and B lose autonomy in relation to each other. If A and B drift apart, the exchange channels between the two systems, as defined in Figure 2, gradually dissipate. A and B lose their autonomy from each other when U = P and L = R, and the two become integrated into a single system. It takes positive feedback, and a qualitative transition for such a situation to materialize from the situation depicted in Figure 2. It is important to stress that the loss of autonomy and the loss of contact are not the only ways in which the constellation including A and B can change. This model does not put any constraints on the possible ways in which frames can be transformed.

A differentiation of two systems A and B does not require us to assume that exchanges from A to B take place according to a different frame as those that take place from B to A.. Bateson (1972/1935) defines symmetrical differentiation as a differentiation between system A and system B where both use the same frame for their communication with each other (say, frame Q), i.e., regardless of whether communication goes from A to B or from B to A..The differentiating aspect in this scenario lies in the fact that communications within the two systems take a different frame than the communication between the two systems. (Figure 3). If P were equal to Q, there would be no differentiation between A and B, i.e., A and B would be the same system.It often happens that communication within A and within B takes place according to different frames as well, but it is not necessarily to make this assumption for the two systems to be differentiated.

Bateson also defines a third type of differentiation, namely reciprocal differentiation, where system A and B can exchange information and goods according to either frame Q or frame R.. It could be argued that a frame Z could be invoked, which allows for both Q and R to occur, without altering the nature of the dynamics between the two components. In other words, reciprocal differentiation is a special case of symmetrical differentiation.

In social systems and family systems, symmetrical differentiation occurs when frames used for interaction do not depend on the direction of the exchange. Two couples may interact with each other in ways that do not depend on the direction of the exchange. However, the couples will have a different frame when interacting amongst themselves, than when they do so with each other.

It is not consistent with modern systems thinking to assume, as Bateson appeared to do, that positive feedback brings about differentation, while negative feedback brings about integration. In the scenario depicted in Figure 2, for example, complementary differentiation is maintained by the differences in U and P, and in L and R respectively. Dampening fluctuation within each of those systems would keep the differentiating process going, while positive feedback might change the system into one in which in L = R or U = P, which would integrate the two systems (they merge into one system). The increments in levels fluctuation that come with positive feedback do not necessarily contribute to differentiation, they could also contribute to integration, in cases where systems are already differentiated. In other words, positive feedback increases the likelihood of change (second order), and change can be either a separation, or an integration of systems. In Bateson's writings, differentiation and positive feedback are confounded.

After repeated deviations from a stable pattern in the course of the interactive flow, new attractors will emerge. Once a system has been transformed, we can identify the attractors that were involved, and label them retroactively. However, when levels of fluctuation reach a level where the system enters a bifurcated region, the emergence of attractors is not a predictable process, as new options for stability emerge.

High variability occurs when there is perturbation. In the context of families, examples of perturbing events are economical hardship, disease, divorce, exposure to consequences of natural disaster, and moving to a new neighborhood. Such events require that family systems adjust themselves to changing circumstances, as existing modes of adjustment may not be adequate (Koopmans, 1998a), while at the same time maintaining their integrity as a distinct constellation (Varela, 1979). The high fluctuation that typically accompanies this process yields a bifurcation of attractors out of which new modes of adjustment emerge. The conflicting injunctions that define double bind are an expression of the systemic duplicity that might occur in periods of transition. Figure 4 illustrates the connection between double bind and the dynamics of change. High levels of variability in interactive behavior can be accompanied by double bind near bifurcation regions, as moment to moment interactions cover two basins of attraction. Figure 4 depicts a situation where attractors x₁ and x₃ are associated with two qualitatively distinct frames of interaction (frame #1 and frame #2). The curve in Figure 4a illustrates the degree to which individual communicative expressions are expected to vary from those attractors. When the fluctuation potential reaches theshold level y, a shift from one state to another occurs. This shift ensures that the communicative trajectory stays away from repeller x₂, and it reduces future variability once the system "settles" on the other attractor. Double binds, then, can occur in situations of instability, close to the bifurcation region (see Figure 4b). The ambiguous nature of double bind metacommunication is an indication of the attractor regime in which multiple conflicting frames guide interactive behavior. It is consistent with the theory to argue that children and adolescents within the family constellation are most vulnerable to the consequences of the use of such conflicting frames because they have a less consolidated representation of the model to which the communicative frames within the family should conform.

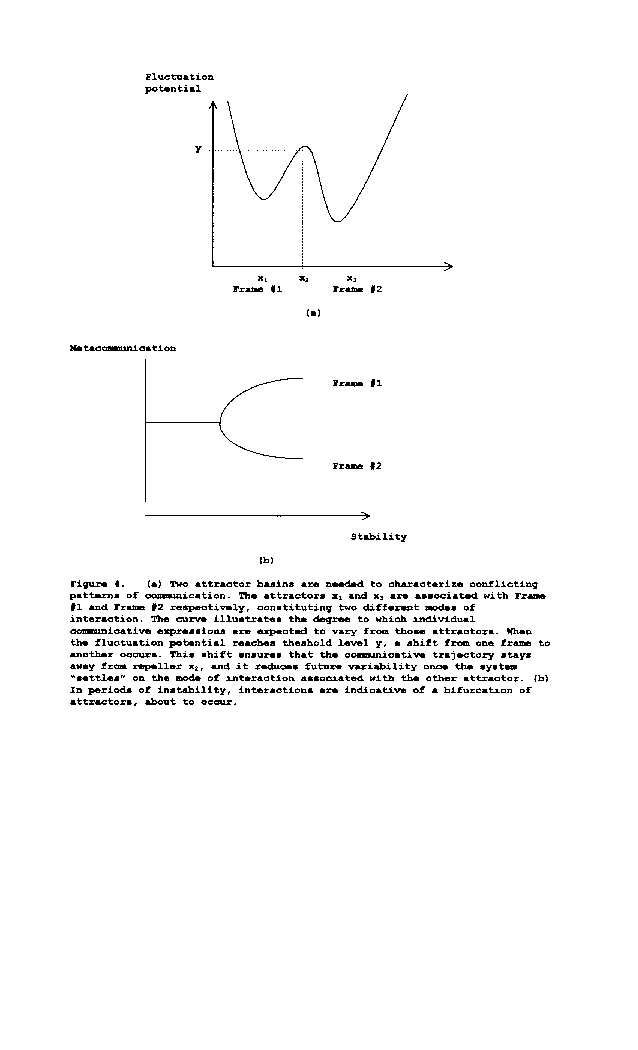
The above description of double bind is not sufficiently specific for it to serve as a predictor of individual psychopathology, schizophrenia or otherwise. Families often go through structural changes in the sense defined above without individual members displaying any symptoms of mental illness. Moreover, ambivalent feelings with respect to significant others is a fact of life for many if not most individuals, many of whom are perfectly healthy. Furthermore, the fact that in periods of fluctuation, there are multiple options with respect to stable interaction does not necessarily imply that those different options are incompatible in the sense of double bind.

There are two aspects to the further specification of double bind. We need to consider the function of communicative attractors more carefully, and we also need to define the attractors involved in double bind more precisely. The subsequent sections address these two questions.

Attractors in communication enable systems to differentiate themselves in the sense defined above. They serve as orientation points when differences between (parts of ) constellations are marked in communication. Family systems, as well as its constituent subsystems, differentiate themselves by a distinct structure, and they keep differentiating themselves in ongoing cycles of interaction. This ongoing process of self-definition in information exchange is consistent with the definition of families as autopoietic systems (Bütz, Chamberlain & McCowan, 1996; Varela, 1979). Autopoietic systems are defined as having a distinct structure, which is continuously recreated through interactive feedback cycles. Furthermore, autopoietic systems subordinate all changes to the maintenance of their own organization (Varela, 1979). Challenges to the integrity of the organization are typically met with a strong stabilizing response.

The definition of families as autopoietic systems has three important consequences insofar as double bind theory is concerned. Firstly, families are defined in terms of how they define themselves: families are distinct from their surroundings because of the ongoing process of self-definition, self-assertion, self-regeneration and self-determination that uniquely characterizes their interaction patterns. The feedback cycles through which this self-affirmation process takes place do not only distinguish a family system from its larger systemic context, but also distinguish subsystems within the family, such as spousal and siblings alliances. Second, and equally important, is the fact that individuals recreate their individuality in the ongoing flow of interaction with the systems of which they are part, including the family and its subsystems (Koopmans, 1998a). Thirdly, double bind illustrates how the expressions of conflicting affect within the family are related to contradictions in this process of self-definition within the system.

Varela called the process of systemic self-determination eigenbehavior. Eigenbehavior refers to behavior through which systems assert their autonomy from other systems. In the family, such assertions involve the affirmation of those relationships, which uniquely distinguish the family system, and a denial of relationships that challenge its structural integrity. Varela's specifies double bind as consisting of two sets: one set consisting of two behavioral states b₁ and b₂, and another set which consists of injunctions operating on those states:

S ₀ = {b₁, b₂} (e.g., love and hostility)

One could fill in this category with any of the particular injunctions that occur within the string of communicative expressions. This definition distinguishes double binds from those situations where multiple definitions of relations are not operated upon by a denial. For example, two sets with S ₀ = {anger, love}, and S _k = {or} do not constitute a double bind because, while there are two definitions, the accompanying injunctions do not bring them into conflict with each other. What distinguishes double binds from other situations of high fluctuation within a system is that the eigenbehavior bÑ is the negation of any previous state, i.e.:

bÑ = not(not(not(...))) = not bÑ

This contradiction creates a circular relationship between behavioral states. The mother son interactive sequence cited above illustrates such a circular state between the love and hostility. In the cited example, the denials keep their interaction going back and forth between the two emotional extremes.

Double binds can be defined as a special case of n-tiple binds, which constitute "an infinite tree of operations on a set of n behavioral states, whose eigenbehavior is a new state experienced as undesirable" (Varela, 1979; p. 199). For the love - hostility example of double bind mentioned above, such a tree would look thus:

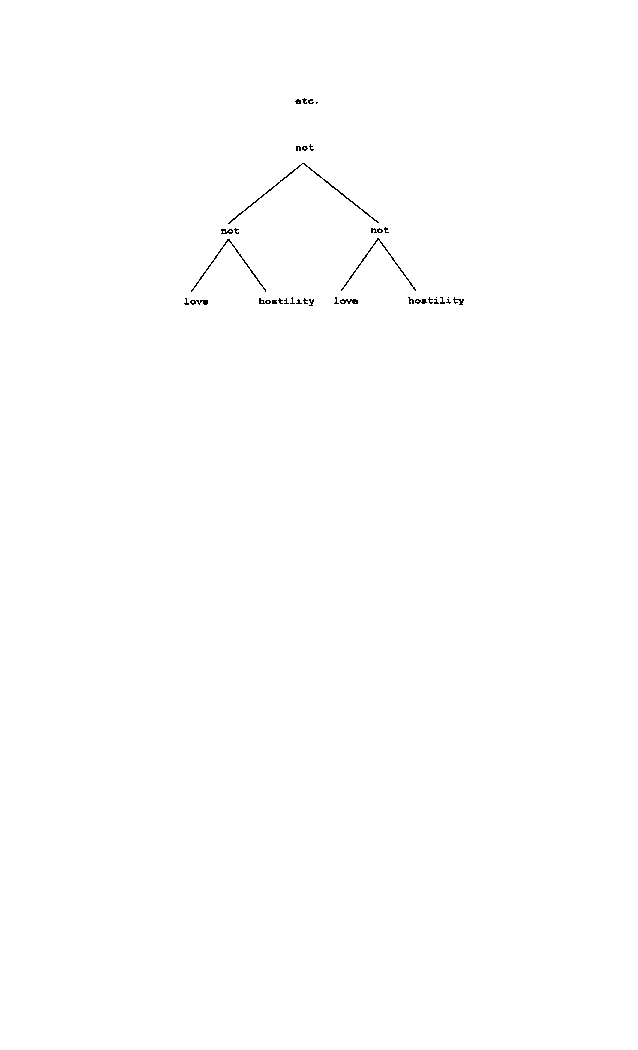
One could also construct a triple bind, including love, anger and hostility as behavioral states, and 'not' as an operator. Since model can be expanded to include more than two or three behavioral states, it is equipped to deal with systemic chaos, involving a large number of attractors. It is important to distinguish those cases where the eigenbehavior is a negation of any behavioral state, as opposed to a conjunction of behavioral states ("b₁ and b₂"), or a disjunction ("b₁ or b₂"). A relatively stable family system can rely on multiple behavioral states as far as their interaction is concerned. N-tiple binds, double or otherwise, create a state of continued instability as the system keeps moving from one attractor basin to the next, and then back again. In systems closer to chaos, the interactive trajectory keeps going back and forth between a larger number of attractors, and the fact that the eigenbehavior is a negation of any behavioral state, prevents the system from settling down.

There is little disagreement about the central importance of contradictions in double bind situations. The idea that paradox in relationships can be pathogenic has become a standard feature in the vocabulary of clinical practitioners. Watzlawick (1965) defines double bind as a 'generic form of paradoxical injunction delivered in a vital ongoing relationship' (quoted in Sluzki, Beavin, Tarnopolsky & Verón, 1967, p.220), and Olson (1972) also considers paradox as an inextricable part of double bind. He makes three important observations concerning relational paradox:

Bateson et al. claimed that double bind theory was based on Russell's paradox (Whitehead & Russell, 1962). Given the importance of the idea of paradox in the clinical literature, the connection between Bateson's work and Russell's paradox requires closer scrutiny (see Appendix A for a formal discussion).

A well known example of paradox is the 'spontaneity paradox' (e.g. Ackerman, 1979). If someone orders someone else to be spontaneous, i.e. "Be spontaneous!" , one could argue that on two different levels, conflicting messages are conveyed. On one level, an injunction is issued, whereas on the other hand, if one follows the injunction, one does not act out of one's own inclination, thereby not following the injunction. Similarly, the injunction 'Don't read this sign' exemplifies a paradox in communication, because the injunction presumes it is being read (Ackerman, 1979). Whether paradoxes such as the spontaneity paradox are of a Russellian type is questionable, however, because, contrary to Russell's paradox, they are not concerned with the problem of defining totality, but simply a conflict between the medium and the message conveyed by that medium (Gundersen, 1988; Roy & Roy, 1987). In the example of the mother son exchange cited above, both the verbal and the nonverbal channels are used to assert and then deny certain sentiments. Rather than being confused about their levels of communication, these two persons are more likely to be confused about their feelings toward one another!

Bateson et al. argued that in the world of logic, different levels of abstraction in the formulation of class - membership relations can be clearly separated, whereas in the world of human communication, this separation will invariably be breached, leading to communication which involves multiple logical types. The best way to think about the breach of logical types in human communication is in terms of Varela's (1979) tree of operations, discussed above. In the case of two binds, we can define a set of two behavioral states, which is included in another set which denies both states, which, in turn, is included in yet another set which denies all that preceded, etc.:

{{{b₁, b₂}not}not}...

Here, the entire set of previous exchanges is denied in each subsequent exchange. The class-membership distinction referred to in Russell's paradox refers in this context to the processes through which behavioral states are asserted, rather than to the question which members are included in the system of interest. While the contradictory nature of this process often plays itself out over different levels of expression (e.g., verbal and non-verbal), it is also possible to have a string of contradictory statements on the verbal - or nonverbal - level alone. The self-perpetuating string of denials breaches logical types in those instances as well. The differences in logical types refer to the specific instances of communicative behavior on the one hand, and the the interactive frame, to which these instances refer, on the other.

Although Russell's paradox may be a good way of characterizing bind interactions, double bind theory does not critically rely on Russell's theory of logical types (Gundersen, 1988; Roy and Roy, 1987). There is no agreement among logicians about the best way to avoid Russell's paradox, and there are many alternatives to Russell's theory of logical types. An example of such alternative would be to specify general principles of classification in such a way that they do not apply for classes which are self-membered (Lemmon, 1965). One can also design methods for the classification of sets and relations that does not require them to be well-formed (e.g., hypersets, Barwise & Moss, 1981). Such resolutions deal with Russell's paradox, without requiring a theory of logical types (Gundersen, 1988; Roy & Roy, 1987).

We have thus far been casual about the definition of attractors involved in metacommunication and double bind. Bateson's example describes double bind in terms of conflicting emotions. Above, we characterized double binds in terms of conflicting relational frames. To understand how the autopoietic process works in families, these emotions need to linked to conflicting self-definitions, and the interaction through which these self-definitions are perpetuated.

There are many ways in which individual families can uniquely assert themselves by way of their rituals, myths, traditions, and so on (Ward, 1995). These myths rituals and traditions establish communicative frames for each part of the system, as well as for the system as a whole. This process does not take place in isolation for each individual family system, because families are embedded in their respective communities. Most families therefore have some critical features in common, such as relationships of descent (parent - child relationships), affinity (spouses), kinship (siblings, extended family), and they typically observe strict rules, mandated by the community, about the separation of these types of relationship (e.g., incest taboo, Levi-Strauss, 1963; 1969). While many variations are possible (e.g., single parent families, adoptive families, etc.) families often have in common that a caretaking responsibility is maintained across generational boundaries, and that there is a separation of relations of affinity on the one hand, and descent and kinship on the other. These relations and distinctions are behaviorally reinforced on an ongoing basis within the family. Through this ongoing reinforcement process, families distinguish themselves from other social systems.

Scholars who are critical of the use of a theory of logical types to describe double bind have suggested that double binds may instead indicate a contradiction in the classification of relationships (Gundersen, 1988; Roy & Roy, 1987). Outside of the context of double bind theory, Lidz and Fleck (1985) have argued that schizophrenic symptoms may be associated with conflicting self-definitions in the family, and may therefore reflect a classification problem. Lidz and Fleck attribute schizophrenic symptoms to the confounding of generational distinctions, and of roles and responsibilities within the family. For example, if parents trapped in an unsuccessful marriage turn to their children for the emotional support they would otherwise seek from their spouses, there is a duplicity in the parent - child relations in that both parent - child, and adult role definitions are reinforced in the interaction between them. There are many different ways in which roles and responsibilities can be confounded in the family, including dissolution of generational boundaries and incestuous role definitions, invoking conflicting frames in the course of interaction. Double bind in that context can be seen as a situation in which two mutually incompatible role definitions, or frames, are reinforced. The incompatibility finds expression in the negative eigenbehavior of the system, an inability of the system to move back or forward, and a high degree of fluctuation occurs within and across communicative levels.

Bateson et al. (1972/1956) hypothesized that double bind is pathogenic if the accurate discrimination of messages conveyed within a double bind context is vitally important. On a metacommunicative level, the most vital discrimination concerns relationships, which define the family as a distinct system, and the spousal, siblings, and caregiving subsystems within it. Especially children and adolescents rely critically on those relationships. It can be readily appreciated that the most effective obfuscation of those vital relationships is their confounding with other relations which are equally vital. Instances in which parent - child relations are confounded with spousal relations are an example. The theories of Bateson and Lidz are highly compatible, in other words. On another level, when family obligations compete with equally compelling priorities in the community (law, citizenship), duplicitous communicative exchanges could be seen as double binds as well (Koopmans, 1997; Rotzien, 1989; Watzlawick, 1963). The strength of the negation, in those instances, is associated with the incompatibility of the two types of relationship. The inability to escape from the situation, postulated by Bateson et al. is associated with the vital importance of the relationships in question.

Structural transitions in the family are not necessarily accompanied by double bind. In most cases of transition, the bifurcation of attractors reduces fluctuation in the interactive flow, by transforming the system from one state to another. For example, once parents have dispensed of their parental role, a period of fluctuation in which the youngster negotiates independence will be typically followed by a transition to a behavioral state where parent and child treat each other as adults. Compare this scenario to a situation in which two self-definitions in the system mutually invalidate each other. If a double bind occurs between parent and child in which both a parent - child, and a spousal definition of the system serve as attractors, the dilemma of the participants has two aspects. (1) The transition to a spousal alliance is unacceptable, and (2) the emergence of the spousal attractor is irreversible. Disengaging from this situation is problematic because of the vital importance of both types of relationships to systemic self-regeneration, and because of the typically high emotional investment of participants into both of these types of relations.

The association between two states in a double bind situation can be captured, then, in the following feedback relation:

The ongoing circular pattern keeps the participants trapped in their contradictory definition of the relational frame on account of which interaction takes place between them. In this situation, a high repellor in the bifurcation region is nevertheless 'crossed' in the interactive flow as the strength of the negations of both behavioral states keeps the system in an ongoing state of turbulence.

With respect to the mother - son exchange mentioned above, a further specification of double bind in terms of the incompatibility of systemic self-definitions allows us to hypothesize that the exchange reflects a fundamental conflict in the self referential process of the system on account of which the exchange takes place. We would further hypothesize that the nature of this conflict is a confounding of their parent-child relationship and another type of relationship, which is deemed incompatible, such as, for example, a relationship with an erotic connotation. Since people crucially depend on such relations, strong emotional, motivational, and psycho-physiological responses are often attached to them, and there is little tolerance of ambiguity. If reliance on those relations is frustrated, the responses associated with them might become frustrated as well, leading to the kind of ambiguity family display toward each other in double bind interactions.

A case discussion by Laing and Esterson (1964) illustrates the connection between conflicting self-definitions within the system, double bind interactions, and schizophrenic symptomatology. The discussion concerns the case of an eighteen year old girl who was admitted to the hospital completely mute, and, later, rambled about her mother loving her while also trying to poison her. (A clear example of perceiving things in double bind patterns)! The identified patient generally had a confused sense of reality, especially about the relations between herself and members of her family, and heard voices defiling her. Laing and Esterson suggest that the confusion had arisen in part because she had been taught to use family titles inconsistent with those referring to the biological status of the members of her family in the following manner:

BIOLOGICAL STATUS TITLES TAUGHT TO THE CHILD

father uncle

mother mummy

aunt (mother's sister) mother

uncle (mother's sister's husband) daddy, later uncle

cousin brother

(Laing & Esterson, 1964; p. 133)

This example illustrates in a nutshell how relational context and the content of a message can be in conflict with each other. If one calls one's uncle 'daddy', there is a contradiction between the message (calling someone 'daddy'), and the relational context in which this message occurs (an uncle - niece relationship). One can also appreciate how calling a father an uncle constitutes a denial of the father - daughter relationship, i.e., the simultaneous affirmation and denial of parenthood, and the simultaneous affirmation and denial of belonging to two nuclear families. The confounding of logical types in this example occurs because each instance in which one relational context is assumed in the communicative exchange is invalidated by all that came before. The conflict between levels, then, concerns the denial in one particular instance of either of the two relational arrangements in context of the entire string of denials that came before.

One can appreciate the dilemma of this system: the identified patient is expected to internalize that her father is not her father, that her uncle is not her uncle, her parents not her parents, and so on. Another example of such an incompatibility of relationships would be interactions which violate the taboo on incest, which dictates that reproductive relationships are incompatible with relationships of descent (Levi-Strauss, 1963; 1969). It should be parenthetically noted that an association between mental illness and incestuous role definitions within the family has been frequently suspected (e.g., Freud, 1955/1896), but that testing the hypothesis appears to fall outside of the purview of current psychological and psychiatric research.

If the relations of concern are vital, as they are in this example, the result of these conflicting assumptions is that two relations of vital importance are invalidated, as situation called transactional disqualification (Sluzki et al, 1967). If two conflicting premises exist with respect to the relationship within a given system, the affirmation and the denial of those premises can both be legitimately derived. This principle, which is called Reductio ad Absurdum (see Appendix B), is consistent with the notion of double bind as a negation of any behavioral state on the adaptive trajectory of the system. Reductio ad Absurdum also provides a rationale for the self-perpetuating nature of negative eigebehavior. There is something intrinsic in eigenbehavior that disallows negation.

Bateson et al. postulated that under prolonged exposure to double bind contingencies, individuals will gradually learn to perceive their environment in bind patterns. One can also state this postulate in terms of autopoietic behavior: The eigenbehavior of the system in which double bind occurs generalizes to the eigenbehavior of the self of a single individual. To the extent that the individual's self-definition is connected to the eigenbehavior of the vital systems in which he or she participates, interaction within those systems concerns the eigenbehavior of individuals with respect to their own individuality as well. If an individual is exposed to conflicting role definitions in relation to his or her parents, negative eigenbehavior in the definition of that system generalizes to the definition of individuals themselves. Negative eigenbehavior with respect to the self produces an empty set (Varela, 1979). But the individual keeps repeating the cycle because the self cannot be annihilated, while at the same time being present to define itself as non-existent (see Figure 6).

S ₀ = {b₁, b₂} S ₀ = {self}

S ₁ = {not} S ₁ = {not}

not self

b₁ b₂ Þ not

In social systems, families in particular, attractors provide the most stable options for the systems' behavior (Koopmans, 1998a; Baron, Amazeen & Beek, 1994). In periods of high instability, new attractors emerge as the system enters the bifurcation region, and interactive behavior becomes less predictable (see Koopmans, 1998a; 1998b for a more extensive discussion). A tranformation of the system reduces instability. Double bind characterizes a situation where two attractors are incompatible, and the system remains in a state of high fluctuation. Not all interaction oriented toward two attractors is double bind interaction. For interactions to be double bind, the two attractors need to be incompatible, where a transition to state 2 is seen as incompatible with the systems integrity, and the emergence of state 2 into the interactive behavior of the system precludes a return to state 1 (irreversibility). In bind situations, the system keeps going back and forth, unable to move on to what was to become, or to return to what used to be. Since double bind theory concerns itself with the etiology of schizophrenia, the question where double binds come from is important. This paper connects double bind with two self-regulatory processes:(1) high fluctuation and the emergence of new attractors, and (2) incompatibility of the new attractor with the survival of system.

The contradictory state of affairs depicted above invokes a logical principle called Reductio Ad Absurdum, which permits the simultaneous affirmation and denial of conflicting assumptions. In the context of relationships of vital importance such a simultaneous affirmation and denial frustrates the individuals' ability to rely on those relationships. Because of the vital importance of the relationships involved, participants are also unable to escape from the conflict. In the ongoing cycle of denials of any behavioral state that occurs, each subsequent denial concerns the entire interactional history of the system. Bateson rightly invoked Russell's paradox to characterize this state of affairs. Russell's paradox describes a contradiction in class-member relationships if a total class is included as its own member. In the context of human interaction, this paradox characterizes the classification of the interaction process itself. The particular instances in the moment to moment interactional flow constitute one level of understanding, while the (conflicting) interactional history constitutes another. In the course of the interactional flow, conflicting information is conveyed on different levels of expression, such as the verbal and the nonverbal level. It is incorrect to suggest, however, that the verbal an nonverbal levels are examples of logical types. Logical types concern the relationship between the moment to moment instances of metacommunicative expression on the one hand, and the frame, which is used to disambiguate those expressions on the other. Whether Russell's theory of logical types is the best way to resolve contradictions of this nature is open to debate. Other resolutions of the paradox have been proposed, such as Barwise and Moss' (1981) hypersets, which enable one to work with paradoxes of Russellian type in spite of their circularity. To detect paradoxes of a Russellian type does not require that we assume a theory of logical types.

While Bateson was mostly interested in two-attractor scenarios, Varela (1979) formulates a more general version of the theory, which considers double bind as a special case of n-tiple binds. This generalization extends double bind theory to a model that can handle multiple attractor regimes, including those of chaotic systems. In these latter cases, period doubling creates a highly complex attractor regime, in which the system keeps going from attractor to attractor, and, due to their incompatibility in relation to each other, the system keeps being highly unstable, and interaction continues to be unpredictable. It is important that according to Varela's definition, multiple attractor regimes are bind situations only if negative eigenbehavior is the dynamic behind this unpredictability. The generalization from double to n-tiple binds also enables us to consider the case of single binds, the ongoing affirmation and denial of the individual self. Bateson et al. argued that prolonged exposure to double bind results in the individual learning to perceive the universe in bind patterns. The most important ramification of this learning process is the perception of the self in bind patterns.

Bateson et al.'s referral to the vital importance of an accurate discrimination of messages implicitly refers to what we now call autopoiesis (Varela. 1979). Metacommunication constitutes a process of self-definition and self-assertion through which systems regenerate themselves on an ongoing basis, thus maintaining their separateness and integrity vis-à-vis other systems. The string of denials that characterize bind behavior inherently conflicts with autopoietic behavior, however, regardless of whether the system includes multiple individuals or a single individual. Binds, in sum, describe the existential crisis of a system, whose continued generation through metacommunication is accompanied by its own destruction.

Abeles, G. (1976) Researching the unresearchable: Experimentation on the double bind. In C. E. Sluzki & D. C. Ransom (Eds.) Double bind: The foundation of the communicational approach to the family. New York: Grune & Stratton. Pp. 113-149.

Ackerman, B. L. (1979) Relational paradox: Toward a language of interactional sequences. Journal of Marital and Family Therapy, 5, 29-38.

Baron, R. M., Amazeen, P. G. & Beek, P. J. (1994). Local and global dynamics of social relations. In R. R. Vallacher & A. Nowak (Eds.) Dynamical Systems in Social Psychology. (pp. 111-138). San Diego: Academic Press.

Barwise, J. & Moss, L. (1991) Hypersets. The Mathematical Intelligencer, 13, 31-41.

Bateson, G. (1972/1935) Culture contact and schismogenesis. In G. Bateson Steps to an ecology of the mind. New York: Ballantine. Pp. 61-72. (Reprinted from Man, 35, article 199.)

Bateson, G., Jackson, D. D., Haley, J. & Weakland, J. (1972/1956) Toward a theory of schizophrenia. In G. Bateson Steps to an ecology of the mind. New York: Ballantine. Pp. 201-227. (Reprinted from Behavioral Science, 1, 251-264.)

Bertalanffy, L. von (1968) General Systems Theory. New York: Braziller.

Bütz, M. R., Chamberlain, L. L. & McCowan, W. G. (1996) Strange attractors: Chaos, complexity, and the art of family therapy. New York: Wiley.

Freud, S. (1962/1896) The aetiology of hysteria. In. J. Strachey (Ed., Transl.) The standard edition of the complete works of Sigmund Freud. Vol. 3. Pp. 191-221.

Haller, J. A. (1989) The double bind: Paradox in human behavior. Doctoral Dissertation, Teachers College/Columbia University. Univ. Microfilms 90-02502.

Gottman, J. M. (1993) The roles of conflict engagement, escalation, and avoidance in marital interaction: A longitudinal view of five types of couples. Journal of Consulting and Clinical Psychology, 61, 6-15.

Gundersen, J. H. (1988) The theory of logical types: A cul-de-sac in communication theory. Nordisk Psykiatrisk Tidsskrift, 42, 63-66.

Hinde, R. A. (1995) A suggested structure for a science of relationships. Personal Relationships, 2, 1-15.

Hoffman, L. (1971) Deviation-amplifying processes in natural groups. In J. Haley (Ed.) Changing families. (Chap. 22). New York: Grune & Stratton.

Koopmans, M. (1997) Schizophrenia and the family: Double bind theory revisited. Dynamical Psychology. [On-line] Available: http://www.goertzel.org/dynapsyc/1997/Koopmans.html

Koopmans, M. (1998a) Chaos theory and the problem of change in families. Nonlinear Dynamics, Psychology & Life Sciences, 2, 133-148.

Koopmans, M. (1998b, February) On the predictability of family interaction: Perspectives from chaos theory. Paper presented at the annual meeting of the Eastern Psychological Association, Boston, MA.

Laing, R. D. & Esterson, A. (1964) Sanity, madness, and the family. Harmondsworth: Pelican.

Lemmon, E. J. (1978) Beginning Logic. Indianapolis: Hackett Publ.

Levi-Strauss, C. (1963) Structural Anthropology (Vol. 1). New York: Basic Books.

Levi-Strauss, C. (1969) The Elementary Structures of Kinship. Boston: Beacon Press.

Lidz, T. & Fleck, S. (1985) Schizophrenia and the family Second Edition. New York: International Universities.

Minuchin, S. & Fishman, H. C. (1981) Family therapy techniques. Cambridge, MA: Harvard University Press.

Olson, D. H. (1972) Empirically unbinding the double bind: A review of research and conceptual formulations. Family Process, 11, 69-94.

Proskauer, S. (1996, June) Feedback, chaos, and family regulation. Paper presented at the annual meeting of the Society for Chaos Theory in Psychology and Life Sciences. Berkeley, CA.

Rotzien, M. K. (1989) A critique of the double bind system: Theory, methodology, and research. Doctoral Dissertation Fuller Theological Seminary, School of Psychology, Univ. Microfilms 89-24359.

Roy, L. & Roy, S. (1987) Does the theory of logical types inform a theory of communication? Journal of Genetic Psychology, 148, 519-526.

Schuham, A. I. (1967) The double bind hypothesis a decade later. Psychological Bulletin, 68, 409-416.

Sluzki, C. E., Beavin, J., Tarnopolsky, A. & Verón, E. (1967). Transactional disqualification research on the double bind. Archives of General Psychiatry, 16, 494-504.

Varela, F. J. (1979) Principles of biological autonomy. New York: North Holland.

Ward, M. (1995) Butterflies and bifurcations: Can chaos theory contribute to our understanding of family systems? Journal of Marriage and the Family, 57, 629-638.

Watzlawick, P. A. (1963) A review of the double bind theory. Family Process, 2, 132-153.

Watzlawick, P. (1965) Paradoxical predictions. Psychiatry, 28, 368-374.

Whitehead, A. N. & Russell, B. (1962) Principia mathematica (abridged version). Cambridge: Cambridge University Press.

Whitchurch, G. & Constantine, L. (1993) Systems theory. In P. G. Boss, W. J. Doherty, R. LaRossa, W. R. Schumm & S. K. Steinmetz (Eds.) Sourcebook of family theories and methods: A contextual approach. New York: Plenum Press. Pp. 325-352.

Russell's paradox refers to a logical contradiction that occurs if one wishes to illustrate one of the most basic principle of classification, namely, that if an object possesses a certain property, it belongs to the class of objects possessing that property. This basic principle is challenged if one considers as an example those classes that are not members of themselves.

More formally, Russell's paradox challenges one of the basic principles of the logic of classification, i.e. the notion that if an object a possesses a certain property F, it belongs the class of objects x possessing that property:

a Î {x: Fx} « Fa (1)

where Î denotes membership, curly brackets enclose a class of objects, and « denotes a biconditional relationship (i.e. 'if and only if'). In words: a is a member the class of x's such that x has the property F, if and only if a has that property F.

Russell's paradox challenges that notion by considering a class that has everything as a member. If we define a class, which has everything as a member, is that class a member of itself? The classes we ordinarily consider are not self-membered. For example, the class of parents is not in itself a parent. To allow for the possibility that classes are not self-membered, we need to identify a class of objects x such that x is not a member of itself:

{x: - (x Î x)} (2)

The minus sign '-' denotes the negation of a proposition (i.e. 'not'), i.e. a class of objects x such that not x is a member of x . By virtue of (1) and (2):

a Î {x: -(x Î x)} « -(a Î a) (3)

In words: a is a member of a class of objects x, such that not x is a member of x, if and only if not a is a member of a. If we call the class of objects, which are not self-membered R, we can substitute R for {x: -(x Î x)}:

a Î R « -(a Î a) (4)

and since (4) holds for an arbitrary a, we can replace a by R as well:

R Î R « -(R Î R) (5)

In words: the class R is a member of R only if R is not a member of R. The principle stated in (1), then, yields a contradiction if one considers classes which are not self membered (adapted from Lemmon, 1965).

Russell sought to avoid contradictions of this sort by proposing a hierarchy of classes, called logical types, where class - membership relations can only be meaningfully described between an object at one level, and a class at the next level highest level of abstraction. The resulting principle, formed the basis for Russell's theory of logical types. The idea of distinguishing logical types to circumvent contradictions of this sort is also one of the conceptual foundations of Bateson et al.'s theory of communication.

From two conflicting assumptions concerning the categorization of object a to A or B, the denial of inclusion of a in either category can be legitimately derived.

Again using Lemmon's (1965) notation, we can express the assumption that if object a is a member of B, that object is not a member of A as follows:

(a Î B) --> -(a Î A) (6)

The conflicting assumption would be:

(a Î B) --> (a Î A) (7)

i.e. if a is a member of B, then a is a member of A as well. If we further assume that a is actually a member of B, i.e.

(a Î B) (8)

it then follows Modus Ponendo Ponens from (1) and (3) that

-(a Î A) (9)

and it follows Modus Ponendo Ponens from (2) and (3) that

(a Î A) (10)

By & Introduction, we may write the conjunction of propositions (4) and (5) as:

-(a Î A) & (a Î A) (11)

The object a is both a member of and not a member of A. Reductio Ad Absurdum permits us to derive from (1), (2), (3), and (6) that a is therefore not a member of B in the first place:

-(a Î B) (12)

With respect to a's membership of B, then, & Introduction permits us to conclude the conjunction of (3) and (7), i.e. that a is a member of B, and a is not a member of B as well:

(a Î B) & -(a Î B) (13)

From (1), (2), (3), and (7), we can derive from (1), (2), (3) and (7) by Reductio Ad Absurdum that a is not a member of A either:

-(a Î A) (14)

From the two conflicting assumptions stated in (1) and (2), the denial of a's membership of A and B logically follows. (Adapted from Lemmon, 1965.)

So if a person a, rightly or wrongly, makes both of these two assumptions about their relationship with another person, the denial of both relationships logically results, together with their affirmation.