DynaPsych Table of Contents

 

 Autobiographical Memory Bump:

A Dynamic Lifespan Model

 

Johannes J.F. Schroots[1]

Department of Psychology, Free University Amsterdam

vd Boechorststraat 1, 1081 BT Amsterdam, The Netherlands.

jjf.schroots@ psy.vu.nl

 

Cor van Dijkum

Department of Methodology and Statistics, Utrecht University

The Netherlands

 

Acknowledgement: We thank E.N.A. van Rossum for drawing the figures, and M.H.J. Assink, J.F. Orlebeke and F.E. Yates for comments on the manuscript. Much of the work reported in this paper was privately funded by ERGO (European Research Institute on Health and Aging).

 

Abstract

 

Autobiographical memory obeys generally to classic principles of remembering and forgetting, in which the distribution of memories follows a power function. Contrary to this is the puzzling ‘bump’ phenomenon of disproportionally higher recall of memories for the period of 10 to 30 years, as observed in middle-aged and older adults. Computer simulation of the dynamic relations between past events (memories) and future events (expectations) shows that lifespan processes of neural growth and decline offer the first satisfactory account for the dynamics of the autobiographical memory bump. A dual process theory of ontogenesis is proposed, stating that the bump reflects the lifespan forces of development and aging, which might also account for the differential course of other neurobehavioral functions.

The purpose of this paper is to develop a dynamic model of the autobiographical memory bump across the lifespan. Autobiographical memory (AM) can be broadly defined as a type of episodic memory for information related to the self, both in the form of memories (retrospective AM) and expectations (prospective AM). If retrospective autobiographical memory relates to the retrieval of memories, experiences or past events in the present (Crovitz & Schiffman, 1974; Rubin, 1986), then prospective autobiographical memory is concerned with the retrieval of expectations, anticipations or future events, which likewise are based on present memory functioning (Maylor et al., 2002; Schroots, van Dijkum & Assink, 2004). Retrospective AM is commonly studied by asking individuals to freely recall events from their own lives and then plot the events according to age at encoding. The technique for studying prospective AM has its origins in the administration of a so called ‘time line’ (Rappaport, Enrich & Wilson, 1985), on which the individual is requested to indicate significant life events for both past and future.

 

On first thought it seems plausible that autobiographical memory obeys to classic principles of remembering and forgetting  (Bartlett, 1932; Ebbinghaus, 1885/1964), in which the distribution of events follows a power function (Rubin & Wenzel, 1996), similar to the classic forgetting or retention curve. Contrary to these principles, however, is the ‘bump’ phenomenon of disproportionally higher recall of memories for the period of 10 to 30 years, as observed systematically in individuals older than about 35 years. It’s the period from which peoples’ favorite films, music, and books come and the period from which they report the most important life-events to have happened (Conway & Pleydell-Pearce, 2000; Rubin, Rahhal & Poon, 1998).

 

So far, a satisfactory explanation for the bump is missing, but three theoretical accounts represent a defensible point of view. The first, cognitive account emphasizes the novelty and distinctiveness of experiences occurring during the bump period of life-transitions from rapid change to stability; the second, narrative/identity account is based on the preferential retention of events from a period of consolidation of the self; and the third, biological/maturational account refers to the general rise and fall of cognitive abilities across the lifespan (for a comprehensive overview see Berntsen & Rubin, 2002). All three accounts derive their interpretative power mainly from descriptive evidence, but fail to give an explanation for the emergence of the bump over the lifespan.

 

Within the framework of the research program ‘Life-course Dynamics’ (Schroots, 2003), we came across some empirical findings, suggesting a dynamic account of autobiographical memory as a system of  both retrospective and prospective memory, subject to continuous changes across the lifespan. In 1998, Schroots and Assink expressed the relative capacity of retrospective and prospective AM in the so- called Principle of the Constant Life Perspective, i.e., the sum of past and future autobiographical events is constant across the lifespan. In the following comparative study of three age groups (young, middle-aged and older adults) with two different AM measures (LIM|Life-line Interview Method; Time-line) for both past and future events, we further developed the principle and came to the conclusion that the relation between past events (PE) and future events (FE) changes systematically with age, while their sum is constant over the lifespan (Schroots et al., 2004). After converting the numbers of events into percentages per age group (Figure 1), we then hypothesized that the ratio of PE (or FE) and the sum of PE and FE with age follows a power curve in which there is a limit to growth (or decline), i.e., the S-shaped, logistic growth or decline curve (van Geert, 1994, p. 101). In other words, the relative number of future events (expectations) decreases with age, whereas the relative number of past events (memories) increases over time, both increase and decrease following the same dynamic pattern within the constraint of the human lifespan.

 

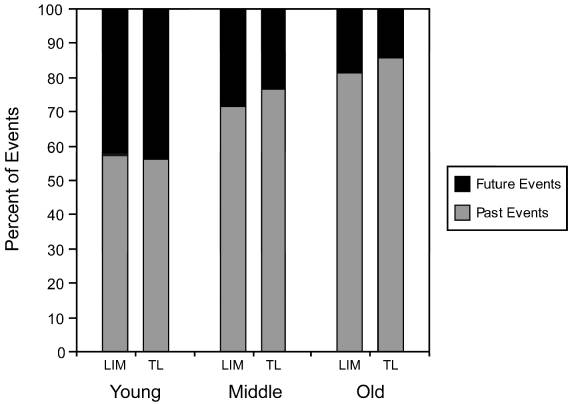
Figure 1.

Ratio of past and future events (percents) for LIM (Life-line Interview Method)

and TL (Time Line) by age group (young, middle, old).

LIM data from Schroots et al., 2004; TL data from deVries and Watt (1996).

 

In the following we will show that the relative distributions of PE and FE follow a retention curve, but also reflect an autonomous growth and decline process, producing the autobiographical memory bump, which – dependent on the parameters of growth and decline – slowly emerges from the forgetting curve. To this end, we will (a) construct and simulate a model which represents, both graphically and mathematically, the dynamics of autobiographical memory across the lifespan, and (b) validate the simulated model against the LIM data set, used for the above-mentioned comparative study, which is summarized in the Methods section.

 

Methods

 

Life-Line Interview Method

 

In a typical LIM session the subject is shown a board with a blank piece of paper, A4 landscape format, on which a grid is printed. The grid consists of a bottom and top line (296 mm), connected by two solid and one dotted vertical line of equal length (180 mm) at 0 mm, 180 mm and 296 mm from the origin, respectively. The space, left from the vertical line at 180 mm, is meant for drawing the past life-line; the space right from the vertical is meant for the future life-line.

 

After presenting three examples of life-lines, from simple to complex and symbolizing the lives of individuals with its ups and downs, the subject is asked to draw without much thought his own life-line for the past from birth dot (middle of vertical line, 0 mm) to his calendar age (vertical line, 180 mm). Next, the subject is asked to label each peak and each dip, i.e. the series of life events, by chronological age and to tell briefly what happened at a certain moment or during an indicated period. After the past life-line has been labeled and described,  the future is explored in the same manner. Starting from the age point where the past life-line has stopped, the subject is asked to continue the line until the dotted age-line (296 mm) of expected death and then to label and describe the peaks and dips of the future life-line. Administration time of the life-line amounts to about 10 minutes. After the session, the peaks and dips (events) in the past and future life-line are scored as PE and FE, respectively. The final result is – briefly summarized – a series of important life events, labeled by chronological age, for both past and future of the individual.

 
Comparative study: Summary

 

In a comparative study of Life-line Interview Method and Time-line, Schroots et al. (2004) explored the distribution of retrospective and prospective autobiographical memory data across the lifespan, in particular the ‘bump’ pattern of disproportionally higher recall of memories from the ages 10 tot 30 years, in conjunction with the well-known recency effect.

 

Ninety eight subjects were interviewed with the LIM, 47 males and 51 females, drawn in almost equal numbers from three age groups: early, middle, and late adulthood. The mean ages and age ranges for the three groups were 23.5 (18-30), 43.3 (31-55), and 67.3 (56-84) years, respectively. The subjects were Caucasians of primarily middle to higher socioeconomic status, recruited initially from educational and health organizations in two Dutch metropolitan areas and then sampled by means of the snowball method.

 

The memory patterns of the LIM data set, originating from this sample, were compared to the published data patterns of the Time-line (deVries & Watt, 1996). The results of this comparative study confirmed the universality of the ‘bump’ for older adults, as well as the recency effect. From the LIM data patterns it was hypothesized that both bump and recency effects play a part not only in middle-aged and older adults, but also in younger people. In search for an explanation of these patterns, it was suggested to study autobiographical memory from a dynamic perspective.

 

Results

 

Construction and simulation

 

Mathematically, the flow (E) from FE to PE, i.e., the dynamic relation between PE and FE, can be expressed in a simple differential equation (1), as articulated for instance in population dynamics for processes of limited growth (Zill & Cullen, 1997). Computer simulation (STELLA, 2000) of this basic (b) model over a period of 100 years shows that the relative distributions of PE and FE follow two crossing patterns of a limited growth and decline curve, respectively, with a small, bell-shaped distribution of E at the beginning of the life-course (Figure 2, top panel).

 

           (Formula 1)       

 

 

 

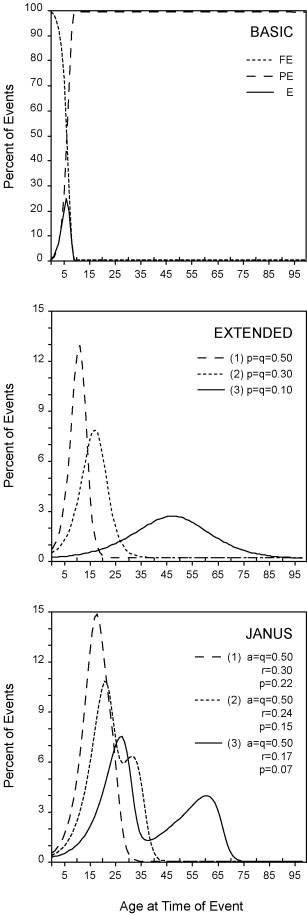
Figure 2.

Three models of event distributions, simulated as a function of reported age at the time of events.

Top panel: Basic model of the distribution of events (percents)(FE = Future Events, PE = Past Events, E = Events).

Middle panel: Extended model for three values of parameters p and q.

Bottom panel: Janus model of the distribution of events (percents) for three sets of parameter values

(fixed values for parameters a and q, and varying values for parameters r and p).

 

 

Rates of growth and decline, as well as the concomitant, bell-shaped curve, may vary across the lifespan. Equation (1) needs to be extended, therefore, with two parameters, p (growth) and q (decline). Simulation of this extended (e) model, based on equation (2), shows that the modus of the bell peaks and moves across the lifespan, dependent on the rates of growth and decline. Estimates of plausible parameter values as presented in Figure 2 (middle panel) are partly based on trial and error, partly on the results of a meta-study on biological aging, which concluded that the average rate of decline from age 30 to 70 years is circa 0.5 % per year (Sehl & Yates, 2001).

          (Formula 2)

In this model the retention curves of PE and FE follow a limited growth and decline curve, respectively, with a concomitant bell-shaped curve for E, but the sougth-after bump in the distribution of PE – and consequently a bimodal distribution of E - cannot be produced yet. To generate this bump we hypothesized that the relative distributions of PE and FE not only follow the classic retention curve, but apparently also mimic or reflect some autonomous process of growth and decline, intrinsic to the nervous system and effective over the total lifespan. To make a reasonable case for this, we had to introduce a second process, modeled in the same way as the retention process, and combined them as follows:

 

 +            (Formula 3)

where parameters p and q denote the retention rates for past and future events, respectively, and parameters r and a denote the growth and decline rates of the hypothesized process, i.e., neural encoding of information (equation 3). Starting from the extended model and on the basis of trial and error, parameter values have been selected which produce more or less representative event-distributions for young, middle-aged and older adults as described in the above-mentioned, comparative study (Schroots et al., 2004). Simulation of this so-called Janus (j) model over a period of 100 years, shows for three sets of parameters (1) a distinct unimodal distribution of events around the age of 20 years, (2) a weak bimodal distribution around ages 25 and 35, and (3) a strong bimodal distribution around the ages of 30 and 60 years (Figure 2, bottom panel). The three simulated event distributions of the Janus model, called after the Roman god with two faces – one face looking into the future and one into the past -, might then be interpreted as follows: (1) the retention and encoding curves of young adults show complete overlap, there is only one bump; (2) as people reach middle age, the retention and encoding curves seem to dissociate, a small bump emerges slowly from the original bump; and (3) when people grow older, the dissociation of retention and encoding comes to an end in the form of two bumps, one for encoding, i.e. the sought-after autobiographical memory bump, and one for retention of past and future events.

 

Validation

 

The crucial question arises as to the fit between Janus model and empirical data in terms of parameter values. To answer this question an advanced simulation program (Macey, Oster & Zahnley, 2000) was used that finds those parameter values in the Janus model that minimize the deviation between the model’s output and the LIM data set, i.e., the root mean square of the differences between individual data points in the dataset and the corresponding points of the Janus model as run by the program. In Figure 3 the LIM event distributions (percents; Schroots et al., 2004), sampled per 5 year interval and to be viewed as the distribution of E of the Janus model, are presented for younger, middle-aged and older adults, as well as the corresponding Janus model distributions for specific parameter values (equation 3). On the strength of the Janus model, it was decided to fix the values of parameters a (decline of encoding) and q (retention FE) at 0.5 % per year for all age groups, and to vary the values of parameters r (growth of encoding) and p (retention PE) per age group. Figure 3 shows that the Janus model reproduces the emerging unimodal and bimodal patterns of events across the lifespan quite satisfactory, i.e., the model’s maxima are fitting close to the modus of the observed bumps in the LIM data set. Also the trend should be noted for the parameter values of r across age, i.e., 0.23 (young), 0.20 (middle) and 0.06 (old), respectively; that is, the growth rate of encoding processes decreases with age. No such trend can be observed for the retention rate p, which confirms that the retention rate for past events is independent of age (Rubin & Schulkind, 1997).

 

 

 

 

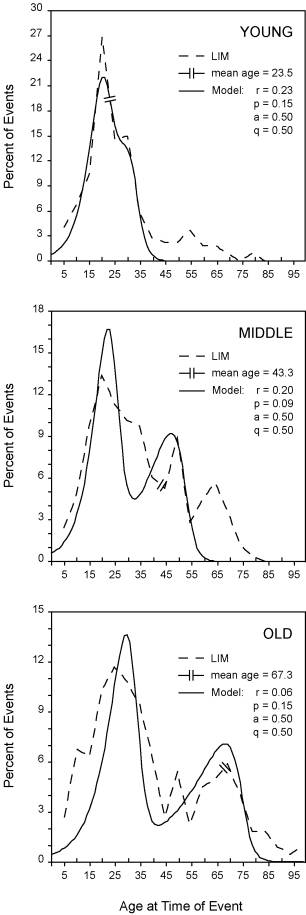
Figure 3.

Fit between Janus model and LIM (Life-line Interview Method) event distributions (percents) per 5 year interval for three age groups.

Fixed values for parameters a (decline of encoding) and q (retention future events); varying values for parameters r (growth of encoding) and p (retention past events) per age group.

Top panel: Young age group (n = 34; mean age = 23.5 yrs; age range = 18 – 30 yrs).

Middle panel: Middle age group (n = 35; mean age = 43.3 yrs; age range = 31 – 55 yrs).

 Bottom panel: Old age group (n = 29; mean age = 67.3 yrs; age range = 56 – 84 yrs).

The graphic symbol for the mean age of each age group, as marked in the LIM event distribution, refers also to the mean transition from past to future events.

 

 

 

Discussion and conclusion

 

By means of the construction, simulation and validation of the Janus model we have demonstrated that processes of growth and decline offer a satisfactory account for the dynamics of the autobiographical memory bump. Decisive for our argumentation is the notion - based on the principle of the constant life perspective -  that the sum of growth and decline is constant over the lifespan according to the simple formula: A + R = L (calendar Age plus Residual lifespan equals the total Lifespan of the individual). From this perspective, growth should be interpreted as the lifelong process of development, measured in years from birth, and decline as the lifelong process of aging, which is traditionally defined in terms of survival and measured in years of residual lifespan from chronological age to (expected) death (Birren, 1959; Comfort, 1956). In general, then, we may conclude that the neurobehavioral function of autobiographical memory is determined by two synchronic processes of ontogenetic change, development and aging.  

 

If the lifespan forces of development and aging generate the autobiographical memory bump via relatively more intensive encoding of information between 10 and 30 years of age, then these forces might also explain the course of other neurobehavioral functions and abilities over the human lifespan, e.g., the differential course of fluid and crystallized abilities. The patterns of both abilities show a rapid rise until early adulthood, followed by a period of relative stability for the crystallized abilities until the age of 60 years, but a slow decline of the fluid abilities after early adulthood (Garlick, 2002; Schaie, 1996). A dual process theory of ontogenesis would explain the differential decline of fluid and crystallized abilities in terms of varied sensitivities for neural processes of growth and senescing. Generally, the growth of the central nervous system comes to an almost complete stop in early adulthood, while the aging of the system or neural slowing continues increasingly. As crystallized intelligence is primarily based on the full grown storage capacity of the central nervous system, which has enormous reserves, crystallized abilities are less dependent on neural slowing than fluid abilities which are primarily related to speed of information processing or neural slowing, rather than to informational capacity. In other words, the differential pattern of crystallized and fluid abilities over the course of life is based on two fundamental processes of change, development (growth) and aging (senescing), of which the parameters determine the final pattern. Further work on the Janus model with regard to other neurobehavioral functions and abilities should be done from this theoretical perspective. 

 

References

 

 

 


[1] Corresponding author